Answer:

The frog enclosure will reach maximum capacity after approximately 15 weeks.
Explanations:
The standard exponential equation is in the form;
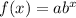
Using the coordinate points (0, 100) and (1, 110) from the table, we can create a system of equation as shown:
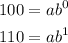
Divide both equations to have:
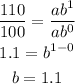
Determine the value of a by substitute the value of b into any of the equation as shown:
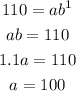
Determine the equivalent exponential function
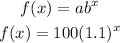
If the maximum capacity is 400 frogs, then f(x) = 400. On substituting into the resulting function, we will have:
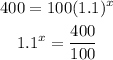
Converting the expression into logarithm function
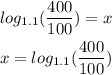
Determine the value of x
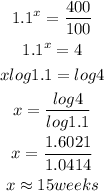
Hence the frog enclosure will reach maximum capacity after approximately 15 weeks.