Question

What is the largest of three consecutive positive integers if the product of the smaller two integers is 12 less than six times the largest integer?

Answer 1

7

Step-by-step explanation:

Let's call the largest of the three consecutive numbers x, so the other two smaller numbers are (x - 1) and (x - 2).

Then, if the product of the smaller two integers is 12 less than six times the largest integer, we can write the following equation:

(x - 1)(x - 2) = 6x - 12

So, if we factorize the expression on the rigth, we get:

(x - 1)(x - 2) = 6(x - 2)

Divide both sides by (x-2):

`\begin{gathered} ((x-1)(x-2))/((x-2))=(6(x-2))/((x-2)) \\ x-1=6 \end{gathered}`

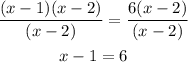
Finally, add 6 to both sides of the equation:

x - 1 + 1 = 6 + 1

x = 7

It means that the largest number is 7, so the three consecutive numbers are 5, 6, and 7. Then, we can verify that the product of 5 and 6 is 12 less than 6 times 7 as:

5(6) = 6(7) - 12

30 = 42 - 12

30 = 30

Therefore, the answer is 7.