Question

Factor the following trinomialx^2+11x+30

Answer 1

The factored form of the quadratic equation is:

`y=a(x-x_1)(x-x_2)_{}`

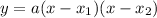
Where x1 and x2 are the roots of the equation.

So, in order to factorate this trinomial, let's find its roots using the quadratic formula:

`\begin{gathered} x^2+11x+30 \\ a=1,b=11,c=30 \\ x_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}=\frac{-11+\sqrt[]{121-120}}{2}=(-11+1)/(2)=-5 \\ x_2=(-11-1)/(2)=-6 \end{gathered}`

So the roots are -5 and -6, so we have:

`x^2+11x+30=(x+5)(x+6)`

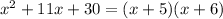
The factored form is (x + 5)(x + 6)