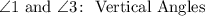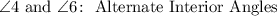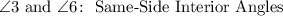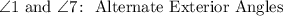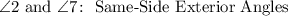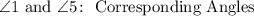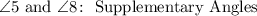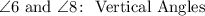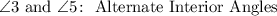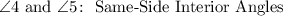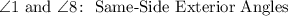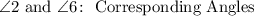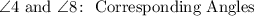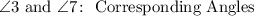Question

Use the figure below to match the type of angles with the correct type of angles.Answer choices:Vertical AnglesComplementaryCorresponding AnglesSame-Side Interior AnglesAlternate Interior AnglesAlternate Exterior AnglesSame-Side Exterior AnglesSupplementary

Answer 1

Given the lines "q" and "r", you can observe that they are intersected by the transversal "p". When this happens, several pairs of angles are formed:

1. Notice that angles 1 and 3 are opposite and they have a common vertex. This indicates that they are Vertical Angles.

2. You can identify that angles 1 and 2 form a Straight Angle (an angle that measures 180 degrees). Therefore, they are Supplementary Angles. This means that:

`m\angle1+m\angle2=180\text{\degree}`

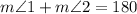
3. Observe that angles 4 and 6 are located between the lines "q" and "r" and on either side of the transversal "p". This means that they are Alternate Interior Angles.

4. Notice that angles 3 and 6 are located between the lines "q" and "r" and on the same side of the transversal. This indicates that they are Same-Side Interior Angles.

5. Having angles 1 and 7, you can observe that they are located outside the lines "q" and "r" and on either side of the transversal. Therefore, you can conclude that they are Alternate Exterior Angles.

6. Notice in the figure that angles 2 and 7 are located outside the lines "q" and "r" but on the same side of the transversal. Hence, you can determine that they are Same-Side Exterior Angles.

7. In the case of angles 1 and 5, you can observe that they are located on the same side of the transversal, but angle 1 is exterior and angle 5 is interior. By definition, a pair of angles with those characteristics are called Corresponding Angles.

8. Notice that angles 5 and 8 formed a Straight Angle. Then, they are Supplementary Angles.

9. Since angles 6 and 8 have the same characteristics as angles 1 and 3, you can determine that they are Vertical Angles.

10. Since angles 3 and 5 have the same characteristics as angles 4 and 6, you can conclude that they are Alternate Interior Angles.

11. Since angles 4 and 5 have the same characteristics as angles 3 and 6, they are Same-Side Interior Angles.

12. Notice that angles 1 and 8 have the same characteristics as angles 2 and 7. Therefore, they are Same-Side Exterior Angles.

13. Having angles 2 and 6, you can notice that they have the same characteristics as angles 1 and 5. Hence, they are Corresponding Angles.

14. In the case of angles 4 and 8, you can observe that they are on the same side of the transversal, but 8 is exterior and 4 is interior. Therefore, they are Corresponding Angles.

15. Angles 3 and 7 have the same characteristics as angles 4 and 8. Then, they are Corresponding Angles.

Hence, the answer is:

`\angle1\text{ and }\angle3\colon\text{ Vertical Angles}`
`\angle1\text{ and }\angle2\colon\text{ Supplementary Angles}`
`\angle4\text{ and }\angle6\colon\text{ Alternate Interior Angles}`
`\angle3\text{ and }\angle6\colon\text{ Same-Side Interior Angles}`
`\angle1\text{ and }\angle7\colon\text{ Alternate Exterior Angles}`
`\angle2\text{ and }\angle7\colon\text{ Same-Side Exterior Angles}`
`\angle1\text{ and }\angle5\colon\text{ Corresponding Angles}`
`\angle5\text{ and }\angle8\colon\text{ Supplementary Angles}`
`\angle6\text{ and }\angle8\colon\text{ Vertical Angles}`
`\angle3\text{ and }\angle5\colon\text{ Alternate Interior Angles}`
`\angle4\text{ and }\angle5\colon\text{ Same-Side Interior Angles}`
`\angle1\text{ and }\angle8\colon\text{ Same-Side Exterior Angles}`
`\angle2\text{ and }\angle6\colon\text{ Corresponding Angles}`
`\angle4\text{ and }\angle8\colon\text{ Corresponding Angles}`
`\angle3\text{ and }\angle7\colon\text{ Corresponding Angles}`