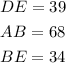For any given Triangle ABC, its medial triangle is constructed by finding the midpoints of its three sides (Segments AB, BC, and AC) and constructing segments to join these midpoints.
An important property of the medial triangle is that it divides the original triangle into four smaller, congruent triangles that are each similar to the original triangle.
With this in mind we now that the four triangles are congruent. Then:
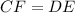
but we know that CF is half of BC, then:
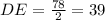
From the figure we also notice that:
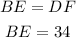
Ans that AB is twice BE, then
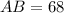
Summing up we have: