Question

A wealthy businessman invests $10,000 and expects a 6.75% rate of return annually. How many years will it take the investment to reach $15,000 in value?Round your answer to the nearest number of years.

Answer 1

7 years

Step-by-step explanation

Given:

Principal, P = $10,000

Rate, R = 6.75%

Amount, A = $15,000

What to find:

The years will it take the investment to reach $15,000 in value.

Step-by-step solution:

You need to first calculate the total interest on the investment using;

Interest, I = Amount, A - Principal, P

Interest, I = $15,000 - $10,000

Interest, I = $5,000

The final step is to find the years it takes the investment to reach $15,000 in value using simple interest formula.

`\begin{gathered} S.I=(T* P* R)/(100) \\ \\ \Rightarrow T=(S.I*100)/(P* R) \end{gathered}`

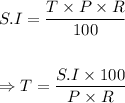
Putting the values of the parameters into the formula, we have;

`\begin{gathered} T=(5000*100)/(10000*6.75)=(500,000)/(67,500)=7.407\text{ }years \\ \\ To\text{ }the\text{ }nearest\text{ }number\text{ }of\text{ }years, \\ \\ T=7\text{ }years \end{gathered}`

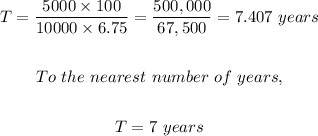
Therefore, it will take 7 years for the investment to reach $15,000 in value.