Question

Find an equation of the line parallel to y=2x-6 that passes through the point (3,-8) if possible write the equation in slope intercept form

Answer 1

Given the equation:

`\text{ y = 2x -6}`

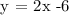
The equation is at Slope-Intercept Form: y = mx + b and the m in the equation represents the slope of the line. Therefore, the slope of the line that represents the equation y = 2x - 6 is 2.

It's been given that the equation of the line that we are looking for is parallel to y = 2x - 6 and passes through the point (3, -8). Thus, we will adapt the slope of the equation and determine the y-intercept by substituting the coordinates in the slope-intercept formula y = mx + b.

We get,

`\text{ y = mx + b}`

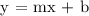
At slope, m = 2 and x,y = 3, -8:

`-8\text{ = (2)(3) + b}`
`-8\text{ = 6 + b}`
`\text{ b = -8 - 6 = -14}`

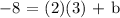
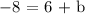
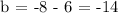
Let's substitute m = 2 and b = -14 to y = mx + b to complete the formula:

`\text{ y = mx + b}`
`\text{ y = (2)x + (-14)}`
`\text{ y = 2x - 14}`

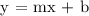
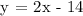
Therefore, the equation of the line parallel to y = 2x - 6 and passes through (3, -8) is

y = 2x - 14.