Answer:
The top of the ladder is moving 1.33 ft per second downwards
Explanations:
Let the height of the ladder be l
Let the distance of the ladder to the wall be x
x = 8 ft
Let the distance from from the top of the ladder to the bottom be d
d = 10 ft
The illustration can be shown by the diagram below:
To find the distance d, use the Pythagorean theorem:
![\begin{gathered} 10^2=l^2+x^2 \\ 10^2=l^2+8^2 \\ l^2=100-64 \\ l^2=36^{} \\ l\text{= }\sqrt[]{36} \\ l\text{ = 6 ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yh8p9r819gk5vccg6mlqwz4iloj2oiuabu.png)
Now, to calculate the speed of the ladder from the top to the bottom, find the derivative of the equation l² + x² = 10² with respect to the time t
The equation becomes:
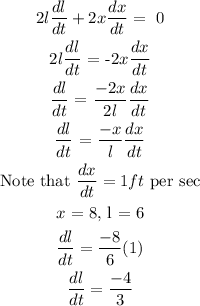
dl/dt = -1.33 ft/s
This means that the top of the ladder is moving 1.33 ft per second down