Question

A person invests $6,750 in an account that earns 5.25% annual interest compounded continuously. Findwhen the value of the investment reaches $15,000. If necessary round to the nearest tenth.The investment will be reach $15,000 in approximatelyyears.

Answer 1

`\begin{gathered} \text{Given} \\ A=15000 \\ P=6750 \\ r=5.25\%\rightarrow0.0525 \end{gathered}`

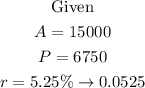
Recall the formula for the Future value of a principal amount, compounded continuously.

`\begin{gathered} A=Pe^(rt) \\ \text{where} \\ A\text{ is the Future Value} \\ P\text{ is the Principal amount} \\ r\text{ is the rate in decimals} \\ t\text{ is time in years} \end{gathered}`

Rearrange the equation so that we can solve for time t.

`\begin{gathered} A=Pe^(rt)^{} \\ (A)/(P)=(Pe^(rt))/(P) \\ (A)/(P)=e^(rt) \\ e^(rt)=(A)/(P) \\ \ln e^(rt)=\ln \mleft((A)/(P)\mright) \\ rt\ln e^{}=\ln \mleft((A)/(P)\mright) \\ rt^{}=\ln \mleft((A)/(P)\mright) \\ (rt)/(r)=(\ln ((A)/(P)))/(r) \\ t=(\ln((A)/(P)))/(r) \end{gathered}`

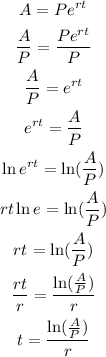
Now substitute the following given and we have

`\begin{gathered} t=(\ln((A)/(P)))/(r) \\ t=(\ln ((15000)/(6750)))/(0.0525) \\ t=(\ln ((20)/(9)))/(0.0525) \\ t=15.2096704\text{ years} \end{gathered}`

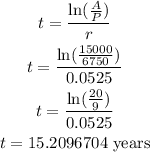
Rounding the answer to the nearest tenth, the investment will reach $15000, in approximately 15.2 years.