Given:
M=(x1, y1)=(-2,-1),
N=(x2, y2)=(3,1),
M'=(x3, y3)= (0,2),
N'=(x4, y4)=(5, 4).
We can prove MN and M'N' have the same length by proving that the points form the vertices of a parallelogram.
For a parallelogram, opposite sides are equal
If we prove that the quadrilateral MNN'M' forms a parallellogram, then MN and M'N' will be the oppposite sides. So, we can prove that MN=M'N'.
To prove MNN'M' is a parallelogram, we have to first prove that two pairs of opposite sides are parallel,
Slope of MN= Slope of M'N'.
Slope of MM'=NN'.
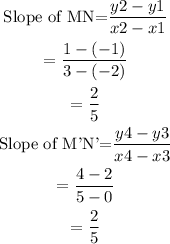
Hence, slope of MN=Slope of M'N' and therefore, MN parallel to M'N'
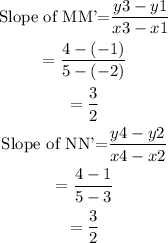
Hence, slope of MM'=Slope of NN' nd therefore, MM' parallel to NN'.
Since both pairs of opposite sides of MNN'M' are parallel, MM'N'N is a parallelogram.
Since the opposite sides are of equal length in a parallelogram, it is proved that segments MN and M'N' have the same length.