Question

A packing carton has a square bottom 18 inches by 18 inches. If the capacity of the carton is 3cubic feet, how deep is the carton?

Answer 1

The packing carton has a square bottom with measures 18in x 18in and has a volume of V=3ft³

The volume of cubic prims can be calculated by multiplying its width by its length and height:

So the formula to calculate the volume is

`V=w\cdot l\cdot h`

If we know the width, length, and volume we can determine the height. First, write the formula for h, that is, divide the volume by the width and height:

`h=(V)/(wl)`

The units of the width and length are in inches and the volume is in cubic feet, to determine the height of the box, all units must be the same. To make the calculations easier I will pass the units from inches to feet.

The unit rate between inches and feet is the following:

`1^(\doubleprime)=(1)/(12)ft`

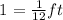
To express 18 inches in feet you have to multiply them by 1/12

`18\cdot(1)/(12)=1.5`

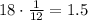
This means that the width and length of the box measure 1.5ft

Now we can determine the height of the box as follows:

w=l=1.5ft

V=3ft³

`\begin{gathered} h=(V)/(wl) \\ h=(3)/(1.5\cdot1.5) \\ h=(4)/(3)ft \end{gathered}`

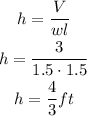
The height of the box is 3/4ft, if you multiply it by 12 you can express the measure in inches:

`(3)/(4)\cdot12=9`

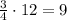
The box has a deph of 9 inches.