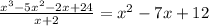we are given the following polynomial:
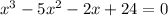
we are asked to use synthetic division by:
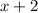
first we need to find the root of "x + 2":
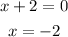
Now we do the synthetic division using the following array:

Now we lower the first coefficient and multiply it by -2 and add that to the second coefficient:

Now we repeat the previous step. We multiply -7 by -2 and add that to the next coefficient:

Now we repeat the previous step. we multiply 12 by -2 and add that to the next coefficient:
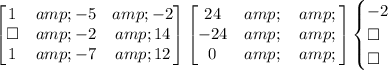
The last number we got is the residue of the division, in this case, it is 0. Now we rewrite the polynomial but we subtract 1 to the order of the polynomial: