Given:
AD is angle bisector of angle BAC.
AB = AC.
The objective is to prove BD = DC.
Step 1:
Statement: AD is angle bisector of angle BAC.
Reason: Given.
Step 2:
Statement:
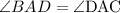
Reason: Definition of angle bisector.
Step 3:
Statement:

Reason: Given
Step 4:
Statement: AD = AD.
Reason: Reflexive.
Step 5:
Statement:
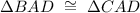
Reason: By SAS criteria.
Step 6:
Statement:

Reason: By Corresponding parts of congruent triangles (CPCT).
Hence, the required results are obtained.