Question

Two pistons are in an enclosed volume with fluid in between them, such that movement in one piston affects the location of the other piston, as shown in the image below if. An explosion occurs in the piston on the left such that it moves 1 m, what is the distance that the piston on the right will move ( assuming that friction can be neglected)? ( Recall that work on an object is equal to the force on the object times the distance is it moved, and that work is conserved

Answer 1

First, we have to set up the necessary equation for work:

`W=\int_(V1)^(V2)PdV`

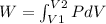
As we can approximate the integral to:

`W=\text{ P*\lparen V}_2-V_1)`

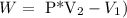
Where V is the volume and P is the pressure.

So, we can calculate these variables:

We have a number 1 state, which is the initial for both pistons (let's call the left piston A and the right one B), and we have the change in the volume that can be shown in the next equation

`\Delta V_=\text{ A*}\Delta\text{S}`

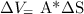
Where A is the transversal area and S is the position. We have the change in the position, so we can calculate the change in the volume:

`\Delta V_A=0.25m^2*\text{ 1m = 0.25m}^3`

Now, we can make these equivalence as the exercise tells that work in conserved:

`\begin{gathered} W=P*\Delta V_A=P*\Delta V_B \\ \\ \end{gathered}`

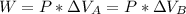
And, if we assume that the process is isobaric (the pressure is the same in both), we can calculate the change in the volume as follows:

`\Delta V_B=\Delta V_A=0.25m^3`

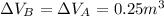
And now, we can calculate the change in the position through the same equation that we used before:

`\begin{gathered} \Delta V=A*\Delta S \\ \\ \Delta S=(\Delta V)/(A)=\frac{0.25\text{ m}^3}{0.5\text{ m}^2}=0.5m \end{gathered}`

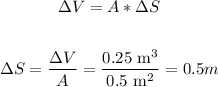
So, the answer is that the right piston moves 0.5m