Question

Find the point where thesetwo linear equations intersect.3x + 5y = 2x + 3y = 4

Answer 1

First step is to write one equation as one variable in terms of another variable.

From the given, we have two equations :

Equation 1 :

3x + 5y = 2

Equation 2 :

x + 3y = 4

Rewrite Equation 2 as the step above.

`\begin{gathered} x+3y=4 \\ x=4-3y \end{gathered}`

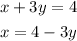
2nd step is to substitute the resulting equation to Equation 1 :

`\begin{gathered} 3x+5y=2 \\ 3(4-3y)+5y=2 \\ 12-9y+5y=2 \\ -4y=2-12 \\ -4y=-10 \\ y=(-10)/(-4)=(5)/(2) \end{gathered}`

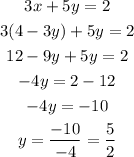
3rd step is to substitute this y value to Equation 2 :

`\begin{gathered} x=4-3y \\ x=4-3((5)/(2)) \\ x=4-(15)/(2) \\ x=-(7)/(2) \end{gathered}`

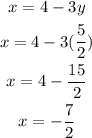
The intersection is at (x, y)

The answer is (-7/2, 5/2)