For the given question, the formula to determine the periodic deposit will be:
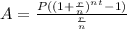
Given:
A= $1,000,000
r = 8.25% = 0.0825
Componded monthly, n = 12
time = t = 40 years
We will substitute with the given values and find the value of P
So,

Rounding to the nearest dollar
so, The periodic deposit = $80
Part (b): we will find the amount comes from the deposit and the amount comes from the interest
The amount of money comes from deposit = 80 * 12 * 40 = $38,400
The amount comes from the interest = 1000000 - 38400 = $961600