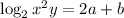Given that: log_(2) \: x =a \: and \: log_(2) \: y= b\: therefore ,expresslog_(2) {} \: x {}^(2) y \: in \: terms \: of \: a \: and \: b

Question

asked Mar 3, 2023 98.5k views

1 Answer

Brian Petro · Answer 1 · 2023-03-07T14:39:45+0000

GIVEN:

The following values are given:

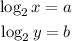
$\begin{gathered} \log _2x=a \\ \log _2y=b \end{gathered}$

We are to evaluate:

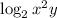
$\log _2x^2y$

CALCULATION:

Step 1: Apply the law of logarithm

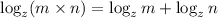
$\log _z(m* n)=\log _zm+\log _zn$

Therefore, we have

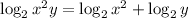
$\log _2x^2y=\log _2x^2+\log _2y$

Step 2: Apply the law of logarithm

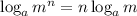
$\log _am^n=n\log _am$

Therefore, the first expression becomes:

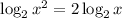
$\log _2x^2=2\log _2x$

Hence, the expression becomes:

$\Rightarrow2\log _2x+\log _2y$

Step 3: Substitute for a and b in the expression above

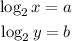
$\begin{gathered} \log _2x=a \\ \log _2y=b \end{gathered}$

Therefore, the expression becomes:

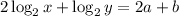
$2\log _2x+\log _2y=2a+b$

ANSWER:

$\log _2x^2y=2a+b$