Question

complete the square and write the equation in standard form. then given the center and radius of the circle.

Answer 1

Circle equation

Given the polynomial

`x^2+y^2+12x-16y=-19`

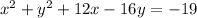
We separate the x and y terms

`\begin{gathered} \lbrack x^2+12x\rbrack+\lbrack y^2-16y\rbrack=-19 \\ \end{gathered}`

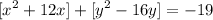
We complete the square equation for each part

First part:

`\begin{gathered} \lbrack x^2+6\cdot2x\rbrack+\lbrack y^2-16y\rbrack=-19 \\ \lbrack x^2+6\cdot2x+36\rbrack+\lbrack y^2-16y\rbrack=-19+36 \\ (x+6)^2+\lbrack y^2-16y\rbrack=17 \end{gathered}`

Second part:

`\begin{gathered} (x+6)^2+\lbrack y^2-8\cdot2y\rbrack=17 \\ (x+6)^2+\lbrack y^2-8\cdot2y+64\rbrack=17+64 \\ (x+6)^2+(y-8)^2=81 \\ \end{gathered}`

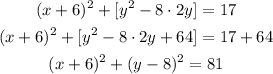
We translate it to the circle equation form

`(x-h)^2+(y-k)^2=r^2`

where (h, k) is the center of the circle and r is the radius

Then, in this case

`\begin{gathered} (x+6)^2+(y-8)^2=81 \\ (x+6)^2+(y-8)^2=9^2 \end{gathered}`

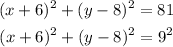
Then it's center is given by ( -6, 8 ) and it's radius is 9