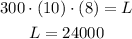Question

13. If four postal clerks require 60 minutes to sort 1,200 letters, how many letters can tenclerks sort in 8 hours?Answer

Answer 1

We must first find the equation that describes the problem:

• P = postal clerks

,

• T = time

,

• L = Letters

`60\min \to1hour`
`\begin{gathered} P\cdot T\cdot C=L \\ \end{gathered}`

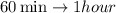
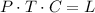
Where C is a constant of proportionality. Then we use the initial values to calculate C

`\begin{gathered} P=4 \\ T=1 \\ L=1200 \\ (4)\cdot(1)\cdot C=1200 \\ C=(1200)/(4) \\ C=300 \end{gathered}`

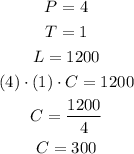
The equation that will help us to calculate the number of letters is

`300\cdot T\cdot P=L`

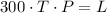
We replace the values of the number of people and the time they had_

`\begin{gathered} 300\cdot(10)\cdot(8)=L \\ L=24000 \end{gathered}`