Question

Can u Please help me review this question by solving

Answer 1

A vector is a specific quantity drawn as a line segment with an arrowhead at one end. It has an initial point, where it begins, and a terminal point, where it ends. The coordinates of a vector can be given by the difference of the coordinates between the terminal point and initial point.

Part A:

A vector can be written in linear form, which is rewrtting the vector as a linear combination of the unitary vectors that generates the vectorial space our vector belongs. In our problem, our points have two coordinates. The unitary vector in the x direction is called i, and the unitary vector in the y direction is called j. Our vectors written in linear form are:

`\begin{gathered} \vec{u}=(8-5)i+(4-16)j=3i-12j \\ \vec{v}=(10-28)i+(16-7)j=-18i+9j \end{gathered}`

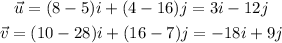
and those are our vectors written in linear form.

`\begin{gathered} \vec{u}=3i-12j \\ \vec{v}=-18i+9j \end{gathered}`

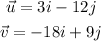
Part B:

A vector written in trigonometric form is similar to the linear form, but the coordinates are parametrized in terms of the angle of the vector and the x-axis.

`\vec{a}=|a|(\cos\theta i+\sin\theta j)`

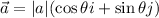
To find the value of this angle first we need to factorize the magnitude of the vector from the linear form. The magnitude is given by the square root of the sum of the squares of the coordinates.

`\begin{gathered} |\vec{u}|=√(3^2+(-12)^2)=√(9+144)=√(153)=9√(17) \\ |\vec{v}|=√((-18)^2+9^2)=√(4\cdot9^2+9^2)=√(9^2(4+1))=9√(5) \end{gathered}`

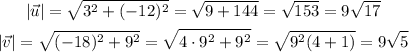
Then, our vectors can be rewritten as:

`\begin{gathered} \vec{u}=9√(17)((3)/(9√(17))i-(12)/(9√(17))j) \\ \vec{v}=9√(5)(-(18)/(9√(5))i+(9)/(9√(5))j) \end{gathered}`

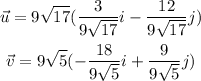
Then, we also know the ratio between the y-coordinate and the x-coordinate of a vector results in the tangent of the angle between the vector and the x-axis.

`\begin{gathered} (u_x)/(u_y)=\tan\theta_u\implies\theta_u=\arctg(-(12)/(3))=\arctg(-4)\approx-75.96^o \\ (v_x)/(v_y)=\tan\theta_v\implies\theta_v=\arctg((9)/(-18))=\arctg(-(1)/(2))\approx-26.57^o \end{gathered}`

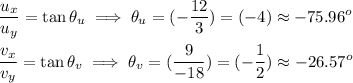
Then, our vectors written in trigonometric form are: