Question

How do you break down an equation to limits if they're cubed and turns out they don't exist?

Answer 1

Looking at the question, if the value of h = 0 is substituted directly into the question, we will obtain an indeterminate form

Method 1

L'Hôpital's Rule can help us calculate a limit that may otherwise be hard or impossible.

So, L’Hospital’s Rule tells us that if we have an indeterminate form 0/0 or

all we need to do is differentiate the numerator and differentiate the denominator and then take the limit.

`\begin{gathered} ((d)/(dx)((2+h)^3-8))/((d)/(dx)(h)) \\ \\ \Rightarrow(3(2+h)^2)/(1) \end{gathered}`

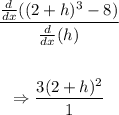
Then we can now put h = 0

`3(2+0)^2`

=> 3 x 4

=> 12

The answer = 12

Method 2

We can expand the numerator and then divide it by the denominator

`\begin{gathered} ((2+h)^3-8)/(h) \\ \\ \frac{8+12h+6h^2+h^3\text{ - 8}}{h} \end{gathered}`

`(12h+6h^2+h^3)/(h)`

`12+6h+h^2`

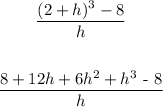
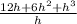
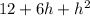
Substituting the value of h = 0

gives 12