The formula for a general term in a geometric sequence is given by
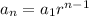
The first term of our sequence is 16, then, our geometric sequence would be
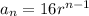
Using the following terms, there's no r that fits for all terms, therefore, this sequence is not geometric.
The general term in a arithmetic sequence is

Where d is the common ratio.
Again, the first term is 16. Using the second term, we can find the value for d.
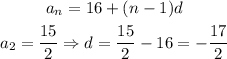
This arithmetic sequence is
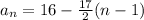
If we evaluate bigger values for n to check with the other given terms, we have a match.
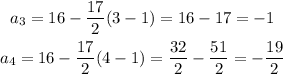
Thus, this series converge because it is arithmetic.