Since Warren takes 4 days to finish the job, then his rate is
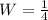
Since Ted takes 6 days to finish the same job, then his rate is
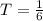
Since Sam takes 2 days to finish the same job, then his rate is
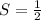
Since Jane takes 5 days to finish the same job, then his rate is

Since all of them will work together to finish the same job, then
The part of each one will be his rate x the time
let the time is t
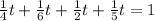
To add the fractions we must make them with the same denominators
Since the LCM of 4, 6, 2, 5 is 60, then
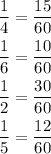
Now we can add them
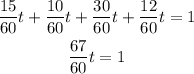
Divide both sides by 67/60 to find t

They need 0.90 days to finish the job if they worked together