Question

If 18 is added to a certain number and sum

Answer 1

We are given that 18 is added to a number. If the number is "n", then we can write this mathematically as:

`n+18`

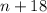
We are also given that the result is divided by 6. This is written as:

`(n+18)/(6)`

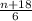
Now, we are given that the result is equal to 1/4 of the number plus 1, this is written as:

`(n+18)/(6)=(1)/(4)n+1`

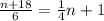
Now, to determine the number we will solve for "n". First, we will distribute the denominator of the fraction on the left:

`(1)/(6)n+(18)/(6)=(1)/(4)n+1`

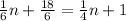
Now, we subtract n/4 from both sides:

`(1)/(6)n-(1)/(4)n+(18)/(6)=(1)/(4)n-(1)/(4)n+1`

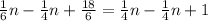
Solving the operations:

`-(1)/(12)n+(18)/(6)=1`

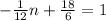
Now, we simplify the fraction on the left side:

`-(1)/(12)n+3=1`

Now, we subtract 3 from both sides:

`-(1)/(12)n+3-3=1-3`

Solving the operations:

`-(1)/(12)n=-2`

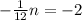
Now, we multiply both sides by -12:

`\begin{gathered} n=(-2)(-12) \\ n=24 \end{gathered}`

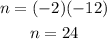
Therefore, the number is 24.