Question

Find the equation of the tangent line to f(x)=6/x at x=-2

Answer 1

`\displaystyle \large{y = - (3)/(2)x}`

Explanation:

Hey there! To find a tangent line of curve at specific point, we have to differentiate a given function. This is because a tangent line has same slope as the specific point and slope is equivalent to dy/dx.

From a given function, we can write as
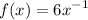`\displaystyle \large{f(x) = 6x^(-1)}` via law of exponent where
`\displaystyle \large{a^(-n)=(1)/(a^n)}` .

Then differentiate with respect to x using power rules.

Power Rules

For every differentiatable continuous functions, if
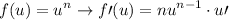`\displaystyle \large{f(u) = u^n \to f\prime (u) = nu^(n-1) \cdot u\prime}` for u is any function and n is all real number.

Therefore:-

`\displaystyle \large{f(x) = 6x^(-1)}\\\displaystyle \large{f\prime(x) = (-1)(6)x^(-1-1) \cdot x\prime}\\\displaystyle \large{f\prime(x) = -6x^(-2) }`

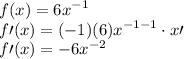
Therefore, our derived function is
`\displaystyle \large{f\prime(x) =- 6x^(-2)}`

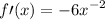
Then substitute x = -2 in a derived function or slope.

`\displaystyle \large{f\prime(-2) = -6x^(-2)}\\\displaystyle \large{f\prime(-2) = -6(-2)^(-2)}\\\displaystyle \large{f\prime(-2) = -6 \cdot (1)/((-2)^2)}\\\displaystyle \large{f\prime(-2) = -(6)/(4)}\\\displaystyle \large{f\prime(-2) = -(3)/(2)}`

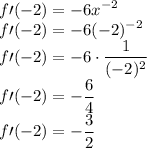
Therefore, the slope at x = -2 is -3/2.

Now we have to use point-slope formula to find the equation of tangent line.

Point-Slope

`\displaystyle \large{y-y_1 = m(x-x_1) \to y-f(x_1) = f\prime (x_1)(x-x_1)}`

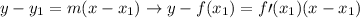
We may have to find the (x,f(x)) coordinate first. We know x = -2 but we don’t know f(x) coordinate at x = -2 yet. We substitute x = -2 in f(x) to find f(-2).

`\displaystyle \large{f(-2) = (6)/(-2)}\\\displaystyle \large{f(-2) = -3}`

Therefore, our coordinate is (-2,-3).

Substitute in point-slope form.

`\displaystyle \large{y-(-3)=-(3)/(2)(x-(-2))}\\\displaystyle \large{y+3=-(3)/(2)(x+2)}`

Then convert to slope-intercept form by isolating y-term and simplify the expression.

`\displaystyle \large{y = - (3)/(2)(x+2)+3}\\\displaystyle \large{y = - (3)/(2)x-3+3}\\\displaystyle \large{y = - (3)/(2)x}`

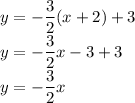
Therefore, the equation of tangent line is y = -3x/2.