We have to calculate the present value of an investment so that we get a future value of $20,000.
The number of periods is n = 10 years, compounded quarterly (m = 4 subperiods per year).
The annual interest rate is 3% (r = 0.03).
Then, we can express the present value PV as:
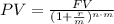
We replace with the values and calculate as:
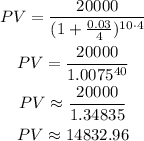
Answer: You will need to deposit $14,832.96.