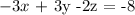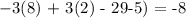To justify that x = 8, y = 2, and z = -5 is the solution to the system,
2x + y + 3z = 3
-3x + 3y - 2z = -8
5x - y + 5z = 13
Let's substitute the roots to the equation if it will be equivalent to the constant value. We get,
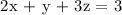
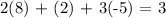
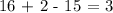
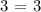
Thus, x = 8, y = 2, and z = -5 is a solution to 2x + y + 3z = 3