Step-by-step explanation
So we have the function f(x):
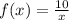
And we have to explain how to obtain its graph from that of y=1/x. The points in the graph of f(x) have the form (x,f(x)) whereas those in the graph of y are (x,y). Then the points in both graphs are given by:
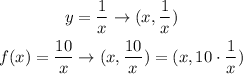
As you can see in order to transform the graph of y into that of f(x) you just need to multiply the y-value of each point by 10.
Now we have to graph f(x). In order to do this we should find several of its points (x,f(x)) but first it's important to note that this graph has a vertical asymptote at x=0 since f(0) is equal to a division by 0 so it's not defined. Now that we have noted this we can take several x values and find some of f's points at the right of the asymptote:
![\begin{gathered} x=1\rightarrow f(1)=(10)/(1)=10 \\ x=2\operatorname{\rightarrow}f(2)=(10)/(2)=5 \\ x=5\operatorname{\rightarrow}f(5)=(10)/(5)=2 \\ x=10\operatorname{\rightarrow}f(10)=(10)/(10)=1 \end{gathered}]()
Then we find points at the left of the asymptote:
![\begin{gathered} x=-1\operatorname{\rightarrow}f(-1)=(10)/(-1)=-10 \\ x=2\operatorname{\rightarrow}f(-2)=(10)/(-2)=-5 \\ x=5\operatorname{\rightarrow}f(-5)=(10)/(-5)=-2 \\ x=10\operatorname{\rightarrow}f(-10)=(10)/(-10)=-1 \end{gathered}]()
Then the graph of f(x) should look like this:
Now we have to give the domain and range of this function. As we saw before this function has an asymptote at x=0 so this point is out of the domain. Then its domain is given by the intervals:
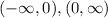
We also need to find its range i.e. all the y-values covered by the graph. As you can see the graph continues towards positive and negative infinite y-values but it seems to have an asymptote at y=0. In order to check this let's see if there's a value of x for which f(x)=0:

If we multiply both sides by x we get:
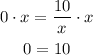
But 0 is not equal to 10. This means that there's no x for which f(x) is equal to 0 and y=0 is not part of the range of f(x). Then its range is:
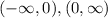
Now we have to find the intervals where the function increases and decreases. In order to see this we can find its derivative. The function increases in the intervals where its derivative is positive and it decreases where it's negative. The derivative of f(x) is:
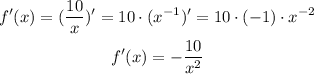
The term 10/x² is always positive so f'(x) is negative for all x in the domain of f(x). Therefore this function always decreases.
Answer
The first answer is: To obtain the graph of f, dilatate the graph of y=1/x by a factor of 10.
The domain of f(x) is: (-∞,0),(0,∞)
The range of f(x) is: (-∞,0),(0,∞)
It increases at: ∅
It decreases at: (-∞,0),(0,∞)