A soccer field has a rectangular figure, this means, the sides of a rectangle form a right triangle with the diagonal, where the diagonal is the hypotenuse. To find the length of a hypotenuse when we know the legs, we can use the Pythagorean Theorem.
The Pythagorean Theorem states that the sum of the square of the legs is equal to the square of the hypotenuse. If we call our diagonal as x, applying this theorem to our problem we have
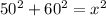
Solving for x:
![\begin{gathered} 50^2+60^2=x^2 \\ 2500+3600=x^2 \\ 6100=x^2 \\ x=\sqrt[]{6100} \\ x=10\sqrt[]{61} \\ x\approx78.102 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k152lry7qnppcpymybyy25wo4op5h8y5zm.png)