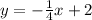Question

Write the equation of the each line in the given formThe line through (3, 8) and (-3, 4) in slope-intercept formThe line through (-5, 4) with slope 2/3 in point-slope formThe line with y-intercept 2 through the point (4, 1) in slope-intercept form

Answer 1

Question 1 (The line through (3, 8) and (-3, 4) in slope-intercept form)

In writing an equation in slope-intercept form, it is important to solve first for the slope of the line. The slope of the line m can be solved using the equation

`m=(y_2-y_1)/(x_2-x_1)`

We have the points (3, 8) and (-3, 4). Substitute the corresponding values on the equation above and solve. We have

`m=(4-8)/(-3-3)=(-4)/(-6)=(2)/(3)`

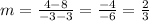
The slope-intercept form of the equation is generally written as

`y=mx+b`

Use one of the points given in the problem and the calculated m. Substitute this on the equation above to solve for b. I will use (3, 8). We have

`\begin{gathered} 8=(2)/(3)(3)+b \\ b=8-2 \\ b=6 \end{gathered}`

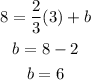
Hence, the equation of the line is

`y=(2)/(3)x+6`

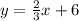
Question 2 (The line through (-5, 4) with slope 2/3 in point-slope form)

The point-slope form of a line is described as

`y-y_1=m(x-x_1)`

Given the slope and the point (-5, 4), we just substitute this on the equation above. The point-slope form is written as

`\begin{gathered} y-4=(2)/(3)(x-(-5)) \\ y-4=(2)/(3)(x+5) \end{gathered}`

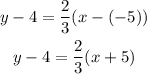
Or we can also rewrite this as

`y-4=(2)/(3)x+(10)/(3)`

Question 3 (The line with y-intercept 2 through the point (4, 1) in slope-intercept form)

In this problem, the y-intercept is given. The y=intercept is represented as b. We also have a point (4, 1). We can solve for the value of the slope of this line using the equation

`y=mx+b_{}`

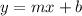
Solving for m, we have

`\begin{gathered} 1=m(4)+2 \\ 4m=1-2 \\ 4m=-1 \\ m=-(1)/(4) \end{gathered}`

Hence, the slope-intercept form of the line is written as

`y=-(1)/(4)x+2`