Question

Use the method of your choice to determine the following probability.Drawing three 9s in a row from a standard deck of cards when the drawn card is not returned to the deck each time.

Answer 1

1/5525

Explanation:

In a standard deck of cards, there are a total of 52 cards.

There are 4 cards labeled 9.

Since the draw is without replacement, the total number of cards reduces after each draw. Therefore:

`\begin{gathered} P(\text{picking the first 9)}=(4)/(52) \\ P(\text{picking the second 9)}=(3)/(51) \\ P(\text{picking the third 9)}=(2)/(50) \end{gathered}`

Thus, the probability of drawing three 9s in a row is:

`P(\text{thre}e\text{ 9s)}=(4)/(52)*(3)/(51)*(2)/(50)=(1)/(5525)`

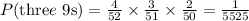
The probability is 1/5525.