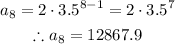Looking at the graph, the three consecutive elements of the sequence are:
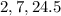
(a)
The common ratio r is the division between two consecutive elements, with the n-th element as the denominator and the (n+1)-th element as the numerator. From the list of elements, the common ratio is:

(b)
The initial value of the sequence is 2, and the common ratio is 3.5, The general recursive formula can be expressed as:
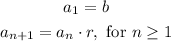
Now, for our problem, we identify b = 2 and r = 3.5. The recursive formula is:
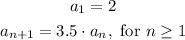
( )
The explicit formula of the sequence is:
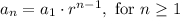
Using the values of a₁ and r:

(d)
The eighth term of the sequence can be calculated if we set n = 8 in the previous formula: