We have to find the extrem values (minimum and maximum) of f(x):
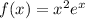
We can find the extreme values by deriving f(x) and equal it to 0 to find the values of x for the extreme points.
To derive f(x) we have to apply the multiplication rule:
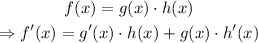
Applied to f(x), we get:
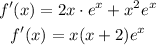
If we equal this to 0 we get:
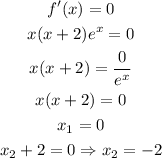
Answer: We have two extrema of f(x): one at x = 0 and the other at x = -2.