The height of the equation is the sea-level hight, so, whenit splashes into the ocean, h(t) = 0. Let's wirte that down:
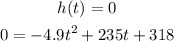
So, the find t for when the rocket splashes into the ocean, we just have to solve for the roots.
We can use Bhaskara's Formula for that:
![\begin{gathered} a=-4.9 \\ b=235 \\ c=318 \\ t=\frac{-235\pm\sqrt[]{235^2-4\cdot(-4.9)\cdot318}}{2\cdot(-4.9)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/smjqv97xjp54kilymkl18zgwdpjnmnblbp.png)
Let's calculate, then:
![\begin{gathered} t=\frac{-235\pm\sqrt[]{235^2-4\cdot(-4.9)\cdot318}}{2\cdot(-4.9)}=\frac{-235\pm\sqrt[]{55225+6232.8}}{-9.8} \\ t=\frac{-235\pm\sqrt[]{61457.8}}{-9.8}\approx(-235\pm247.9068)/(-9.8) \\ t_1=(-235+247.9068)/(-9.8)=(12.9068)/(-9.8)\approx-1.3170 \\ t_2=(-235-247.9068)/(-9.8)=(-482.9068)/(-9.8)\approx49.276 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r10ysqriib4panueqs8tklx1mlzwcxyu29.png)
Since the launch was at t = 0, we can't have a negative value of t, so our answer is t = 49.276 s.
To calculate how high above the sea-level the rocket gets, we can firts find the x value of the vertex of the equation, which will be the highest point. This will be our t.
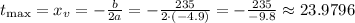
Now, we input this t into the equation for the height:
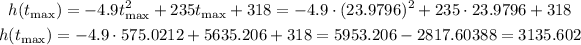
So, the rocket peacks at 3135.602 meters above the sea-level.