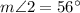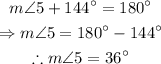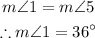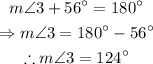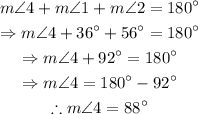Question

I need help find the measures of angles 1,2,3,4 &5

Answer 1

There are some angle relations on the picture that can help answering the problem.

For instance, notice that the two lines which have no marks are parallel, since the two triangles that are formed are similar by the SAS criterion.

Since those lines are parallel, notice the following:

Angles 1 and 5 are corresponding angles. Then, they have the same measure.

Angles 2 and the angle whose measure is 56° are also corresponding angles.

On the other hand, since the angle 5 and that whose measure is 144° are adjacent angles on a straight line, they are suppementary angles. The same is true for the angle 3 and that whose measure is 56°.

Finally, we can find the measure of the angle 4 remembering that the sum of the internal angles of a triangle is always 180°.

From all these considerations, we know that:

`m\angle2=56^(\circ)`
`\begin{gathered} m\angle5+144^(\circ)=180^(\circ) \\ \Rightarrow m\angle5=180^(\circ)-144^(\circ) \\ \therefore m\angle5=36^(\circ) \end{gathered}`
`\begin{gathered} m\angle1=m\angle5 \\ \therefore m\angle1=36^(\circ) \end{gathered}`
`\begin{gathered} m\angle3+56^(\circ)=180^(\circ) \\ \Rightarrow m\angle3=180^(\circ)-56^(\circ) \\ \therefore m\angle3=124^(\circ) \end{gathered}`
`\begin{gathered} m\angle4+m\angle1+m\angle2=180^(\circ) \\ \Rightarrow m\angle4+36^(\circ)+56^(\circ)=180^(\circ) \\ \Rightarrow m\angle4+92^(\circ)=180^(\circ) \\ \Rightarrow m\angle4=180^(\circ)-92^(\circ) \\ \therefore m\angle4=88^(\circ) \end{gathered}`