Question

Find an equation of a line through (−5, 4) and parallel to 3x − 6y = 3.

Answer 1

The equation of a line, in slope-intercept form, is expressed as

`\begin{gathered} y=mx+c\text{ ----- equation 1} \\ where \\ m\Rightarrow slope\text{ of the line} \\ c\Rightarrow y-intercept\text{ of the line} \end{gathered}`

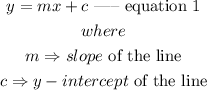
Suppose lines A and B are parallel to each other, their slopes become equal.

This implies that

`\begin{gathered} m_A=m_B\text{ ----- equation 2} \\ where \\ m_A\Rightarrow slope\text{ of line A} \\ m_B\Rightarrow slope\text{ of line B} \end{gathered}`

Given that a line passes through (-5, 4) and is parallel to

`3x-6y=3`

Step 1: Let the equation of line A be

`3x-6y=3`

Step 2: Express the equation of line A in the slope-intercept form as expressed in equation 1.

Thus,

`\begin{gathered} 3x-6y=3 \\ add\text{ -3x to both sides of the equation,} \\ -3x+3x-6y=-3x+3 \\ \Rightarrow-6y=-3x+3 \\ divide\text{ both sides by the coefficient of y, which is -6} \\ -(6y)/(-6)=(-3x+3)/(-6) \\ \Rightarrow y=(1)/(2)x-(1)/(2)\text{ ---- equation 3} \end{gathered}`

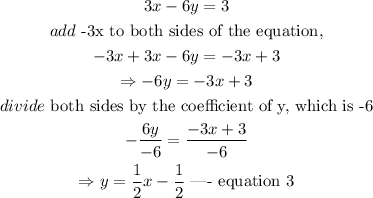
Thus, the equation of line A is expressed as

`y=(1)/(2)x-(1)/(2)`

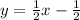
Step 3: Determine the slope of line A.

Comparing equations 1 and 3, we have

`m=(1)/(2)`

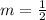
Thus, the slope of line A is

`m_A=(1)/(2)`

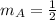
Step 4: Determine the slope of line B.

Recall that lines A and B are parallel,

`\begin{gathered} m_A=m_B \\ \Rightarrow m_B=(1)/(2) \end{gathered}`

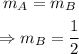
Step 5: Express the equation of line B.

The equation of a line that passes through a point is expressed as

`\begin{gathered} y-y_1=m(x-x_1)\text{ ----equation 4} \\ where \\ m\Rightarrow slope\text{ of the line} \\ (x_1,y_1)\text{ }\Rightarrow coordinate\text{ of the point through which the line passes} \end{gathered}`

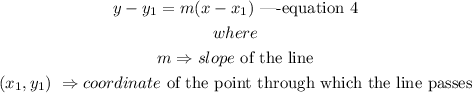
Given that line B passes through the point (-5,4), this implies that

`\begin{gathered} x_1=-5 \\ y_1=4 \end{gathered}`

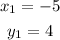
Thus, the equation of the line is expressed as

Hence, the equation of the line is expressed as

`y=(1)/(2)x+(13)/(2)`

The third option is the correct answer.