We are asked to approximate the area under a curve of the following function:
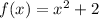
in the interval [0,5], using 5 subintervals. To do that, let's visualize the problem in the following graph.
The idea of the exercise is to find the area of each rectangle and add them all up in order to approximate the area under the curve. To do that, we need first to find the base of each rectangle. Since they all have the same base length, this must be equal to the length of all the bases combine over the number of rectangles, this is:
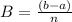
Where b and a, are the extreme points of the interval we are working, in this case, [a,b]=[0,5], replacing we get:
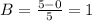
Therefore the base of each rectangle is 1. Now we need to find the height of each rectangle. The height is equal to the function evaluated at the extreme left point of the rectangle, we have the following values:
for x = 0
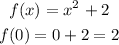
for x = 1
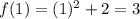
for x = 2
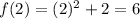
for x = 3
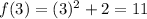
for x = 4
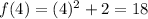
Now we find each area multiplying the base by its height and we add them all together:
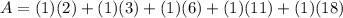
Solving we get:
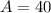
Therefore, the area under the curve is 40