The volume of the cylinder is equal to the product of the height and the area of the base of the cylinder:
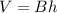
Where
B is the area of the circular base
h is the height of the cylinder
To calculate the area of the circular base, you can apply the following formula:
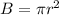
Then you can calculate the volume as follows:
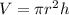
The diameter of the circular base is 7.9mm, the radius is half the diameter, then:
![\begin{gathered} r=(d)/(2) \\ r=(7.9)/(2) \\ r=3.95\operatorname{mm} \end{gathered}]()
You have to calculate the volume in cubic centimeters, so you have to convert the units from millimeters to centimeters.
1 centimeter is equal to 10 millimeters, divide the radius by 10 to determine the equivalent value in centimeters:
![(3.95)/(10)=0.395\operatorname{cm}]()
The height of the cylinder is 18.8mm, to express this value in centimeters, you have to divide it by 10:
![(18.8)/(10)=1.88\operatorname{cm}]()
Once both dimensions are expressed in centimeters, you can calculate the volume of the cylinder:
![\begin{gathered} V=\pi r^2h \\ V=3.14\cdot(0.395)^2\cdot1.88 \\ V=3.14\cdot0.156025\cdot1.88 \\ V=0.92104678 \\ V\approx0.9\operatorname{cm}^3 \end{gathered}]()
The volume of the cylinder is equal to 0.9 cubic centimeters.