52mph
1) We can solve this problem, using one equation:
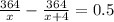
Note that we have used a ratio, in which on the numerator we can write the distance and the bottom number stands for the time. So basically we are writing an expression based on this:
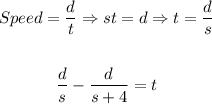
2) Now, let's solve it to find the speed:

As there are no negative velocities, then we can discard the negative root for that and tell that the usual speed is 52 mph