Let x and y be the number of children and adults in the group, respectively. Therefore, the two equations are
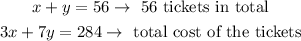
Solve the system of equations as shown below

Solving the former equation for y,
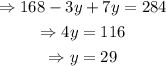
Finding x,

The answer is 27 children and 29 adults in total.