Let 'k' be the scale factor of the two similar figures.
So, 'k' will be the ratio of the linear dimension of the larger figure to the linear dimension of the smaller figure.
Consider that if the linear dimensions of two figures are in the ratio 'k', then the ratio of their corresponding areas will be the square of 'k', and the ratio of their corresponding volumes will be the cube of 'k'.

Given the two surface areas, the value of scale factor can be obtained as follows,
![\begin{gathered} (864)/(486)=k^2 \\ k=\sqrt[]{(864)/(486)} \\ k=\sqrt[]{(16)/(9)} \\ k=(4)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f1mty0w9nqxwxtbbc43l3kbiolq2ky6d2n.png)
It follows that,
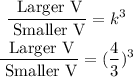
Given the larger volume as 1792 cubic inches, the smaller volume is calculated as,
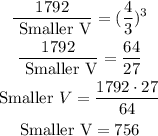
Thus, the smaller volume that is, the volume of the smaller figure is 756 cubic inches.