You need to start by drawing the line segment that connects the points on the function where x=2 and x=7.
As you can see in the graph, these points are located at:
(2, 10) and (7, -5)
Thus, the line segment will look like:
To determine the average rate of change of the function on the given interval you can use the next formula:
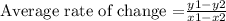
Then, by replacing the coordinates of point 1 and point 2, we obtain:
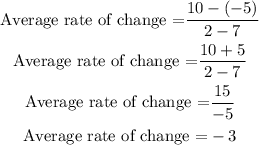
The average rate of change on the interval 2