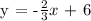Given:
a.) Parallel to a line: 2x + 3y = - 15
b.) Passes through the point (3, 4)
Let's find the equation of a line parallel to 2x + 3y = -15.
Note: Since the line that we are looking at is parallel to 2x + 3y = -15, they should have the same slope.
Step 1: Let's determine the slope of the line based on its slope-intercept form: y = mx + b.
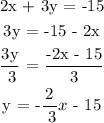
Therefore, the slope of the line (m) is -2/3.
Step 2: Using the slope = -2/3 and x,y = 3,4. Plug it in y = mx + b to find the y-intercept of the parallel line.
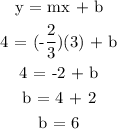
Step 3: Let's now complete the equation. Substitute the slope (m) = -2/3 and b = 6 in y = mx + b.
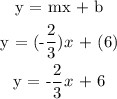
Therefore, the equation of the line parallel to 2x + 3y = -15 is: