A ordered pair is a solution to the system if it satisfies all the equations of the system.
We have to check each equation for each pair.
We start with (-9,-6):

As one of the equation is not satisfied, (-9,-6) is not a solution.
For (7,7) we have:
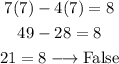
As one of the equation is not satisfied, (7,7) is not a solution.
For (0,-2) we have:
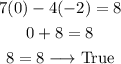
As this equation is satisfied, we test the second equation:

As one of the equations is false, (0,-2) is not a solution.
Now, we test (4,5):
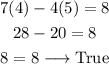
As this equation is satisfied, we test the second equation:
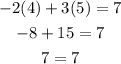
The ordered pair (4,5) is a solution to the system.
Answer:
The only pair that is a solution is (4,5)