Question

Multiple part question Here are the needed details:Five rotations took 5.15 seconds 1 rotation took 1.07s Distance from shoulder to elbow is 29 cm distance from shoulder to middle of the hand is 57cm.7. A. What was the average angular acceleration (degrees/s squared and rad/s squared) of the elbow?B. What was the average centripetal acceleration (m/s squared) of the elbow?C. How do these compare to the hand? Why are they the same and or/ different?

Answer 1

Given data

One rotation means 360 degree

The angular speed for five rotations is

`\omega_1=(5*2\pi)/(5.15)=6.09\text{ rad/s}`

The angular speed for one rotation is

`\omega_2=\frac{1*2\pi^{}}{1.07}=5.86\text{ rad/s}`

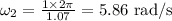
(A)

The average angular acceleration is zero here as there is no change in the angular velocity. But, if you consider that first case (A) where the angular velocity is 6.09 rad/s and the second case where the angular velocity is 5.86 rad/s. You can say that there is a change in angular velocity but there is no particular time interval. Hence, you can not calculate the average angular acceleration. For individual cases, there will be no average acceleration.

But, there will be centripetal acceleration which will act towards the center of the circle.

(B)

The length of the elbow is given as

`r=29\text{ cm=0.29 m}`

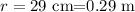
The centripetal acceleration of the elbow is calculated as

`\begin{gathered} a_e=\omega^2_2r \\ =(5.86)^2(0.29) \\ =9.99m/s^2 \end{gathered}`

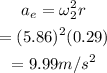
(C)

The length of the hand is given as,

Therefore, the centripetal acceleration on the hand is calculated as

`\begin{gathered} a_h=\omega^2L \\ =(5.86)^2(1.14) \\ =39.14m/s^2 \end{gathered}`

Thus, the centripetal acceleration for the hand is different from the elbow