To solve this problem, we should first find the value of x. To do so, we will use the triangle midsegment theorem and some extra facts that derive from it.
Recall that triangle midsegment theorem states that if we join two midpoints of two sides of a triangle, the line (midsegment) that is formed is parallel to the other side and it has half of its measure.
By using this theorem, in the given drawing, the segment KL is parallel to the segment GI. Since both angles are formed with the segment GH and lines GI and KL are parallel, we end up having the following
That is, the angles that are formed with the line GH and lines GI and KL are congruent and thus have the same measure.
We are told that angle LKH has a measure of 2x+49 and angle JGK has a measire of 4x+29. Since this two angles should be equal in measure, we end up having the following equation
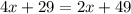
Now, we apply mathematical operations on both sides to "isolate" x on one side of equality sign. We start by subtracting 2x on both sides, we get

Now, we subtract 29 on both sides, so we get
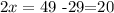
Finally, we divide by 2 on both sides, so we get
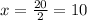
So the value of x is 10. Now, we replace this in the expression of the measure of LKH to find its measure, which is
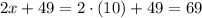
so the measure of angle LKH is 69° degrees