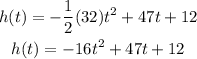To find the maximun height we need the vertex of the quadratic equation,
To calculate it, we use
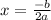
Where x is x value in the maximun value, b is the coefficient of the linear expression and a is the coefficient of the square expression
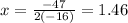
And the y axis is,
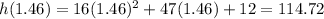
So, to find the maximun height we need the vertex of the quadratic equation. In this case the maximun height is 114.72 feet.
First question)
To write the vertical motion equation we use,
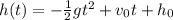
Where g is the gravity, v0 is the initial velocity and h0 is the initial height.
Then, we need to replace the values