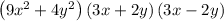Question

What is the completely factored form of this polynomial?81x4 - 16y4A. (3x2 + 2y2)(9x+4y)(9x - 4y)B. (9x2 + 4y2)(9x2 - 4y2)C. (9x2 + 4y2)(3x – 2y)^2D. (9x2 + 4y2)(3x+2y)(3x – 2y)

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given expression

`81x^4-16y^4`

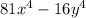
STEP 2: Factorize the expression

`\begin{gathered} 81x^4=(9x^2)^2 \\ 16y^4=(4y^2)^2 \end{gathered}`

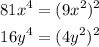
We have:

`\begin{gathered} =\left(9x^2\right)^2-\left(4y^2\right)^2 \\ \mathrm{Apply\:Difference\:of\:Two\:Squares\:Formula:\:}x^2-y^2=\left(x+y\right)\left(x-y\right) \\ \left(9x^2\right)^2-\left(4y^2\right)^2=\left(9x^2+4y^2\right)\left(9x^2-4y^2\right) \\ =\left(9x^2+4y^2\right)\left(9x^2-4y^2\right) \end{gathered}`

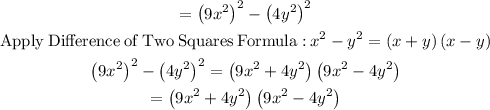
By further simplification, we have:

Factorize the second part:

`\left(9x^2-4y^2\right)=\left(3x+2y\right)\left(3x-2y\right)`

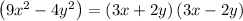
Hence, the final factored form is given as:

`\left(9x^2+4y^2\right)\left(3x+2y\right)\left(3x-2y\right)`