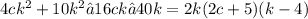Question

4ck^2 + 10k^2 − 16ck − 40kPart A: Rewrite the expression by factoring out the greatest common factor. Part B: Factor the entire expression completely. Show the steps of your work.

Answer 1

We have the following polynomial:

`4ck^2+10k^2-16ck-40k`

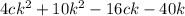
See that 2k is the greatest common factor, then, let's factor it out

`2k(2kc+5k-8c-20)`

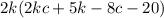
We can still do some small factors inside the parenthesis, like:

`\begin{gathered} 2kc+5k-8c-20 \\ \\ k(2c+5)-4(2c+5) \\ \\ (2c+5)(k-4) \end{gathered}`

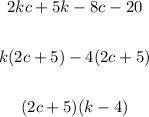
Then, inside the parenthesis it's

`2k(2c+5)(k-4)`

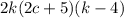
Therefore, the expression, completely simplified is

`4ck^2+10k^2−16ck−40k=2k(2c+5)(k-4)`