Question

Somebody please help me algebra 2 graphing equations!! help me find: ( AND SHOW WORK PLEASE) 1) slope of the initial climb2) domain and range of graph3) equation that represents initial climb4) if it’s a function or not ( why or why not)5) which hill is steeper by determining rate of change of each

Answer 1

1-2) See the picture above.

3) The slope of the line that passes through the points (x1, y1) and (x2, y2) is computed as follows:

`m=(y_2-y_1)/(x_2-x_1)`

The initial climb passes through the points (0,0) and (20, 50), then its slope is:

`m=(50-0)/(20-0)=(5)/(2)=2.5`

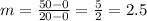
4) The equation of a line in slope-intercept form is:

y = mx + b

where m is the slope and b is the y-intercept

The line of the initial climb intersects the y-axis at the point (0,0), then b = 0.

Substituting with m = 5/2 and b = 0, the equation of the line of the initial climb is:

`\begin{gathered} y=(5)/(2)x+0 \\ y=(5)/(2)x \end{gathered}`

5) The domain is the set of all possible x-values.

The range is the set of all possible y-values.

From the graph:

Domain: [0, 230]

Range: [0, 50

6) The rate of change of a function f(x) between the points x = a, and x = b, is computed as follows:

`\text{ rate of change =}(f(b)-f(a))/(b-a)`

Considering the points (50, 0) and (70, 35), which means

a = 50

b = 70

f(a) = 0

f(b) = 35

the rate of change of the first hill is:

`\text{ rate of change =}(35-0)/(70-50)=(7)/(4)`

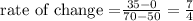
Considering the points (170, 0) and (200, 20), which means

a = 170

b = 200

f(a) = 0

f(b) = 20

the rate of change of the second hill is:

`\text{ rate of change =}(20-0)/(200-170)=(2)/(3)`

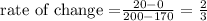
The steeper hill is the first hill because its rate of change is greater.

7) In a function, for every x-value in the domain there is associated only 1 value of y in the range. We can see in the graph that x = 130 is associated with two y-values: y = 25 and y = 3.8. In consequence, the roller coaster is not a function.